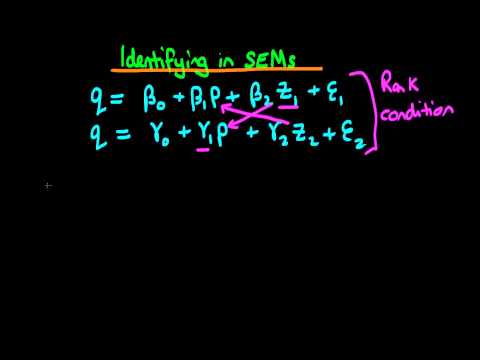Who Form 8655 Reduced 2024

In this video, I want to talk about the conditions under which we can identify parameters in a simultaneous equation framework. In the last video, we spoke about a system whereby we had a supply equation. The quantity supplied (Q) was equal to beta naught plus beta 1 times the price plus beta 2 times an exogenous variable (set 1). We also had a demand equation, where Q was equal to gamma naught plus gamma 1 times the price plus gamma 2 times set 2. Note that I've added another exogenous variable (set 2) to this demand equation, which is in contrast to what we had in the last video. We discussed the fact that we could identify the parameter gamma 1 in the previous example because there was an exogenous variable (set 1) that occurred in the first equation but not in the second equation. So, we were able to use set 1 as an instrumental variable (IV) for the price (P) and estimate the parameter gamma 1. Similarly, in this case, we can use set 2 as an IV for P in the first equation, since set 2 is an exogenous variable that doesn't occur in the first equation but does occur in the second equation. Under this setup, we can identify parameters if a condition known as the rank condition is met. The rank condition states that for each particular equation, there must be at least as many exogenous variables included in that equation that can act as IVs for each of the endogenous variables in that equation. Let's go through an example to make everything clearer. Let's say we have a simultaneous equation setup where Y1 = beta naught + beta 1 times Y2 + some exogenous variables (Z1, Z2, Z3) + error term (epsilon 1). The second equation...