Can Form 8655 Resolve 2024

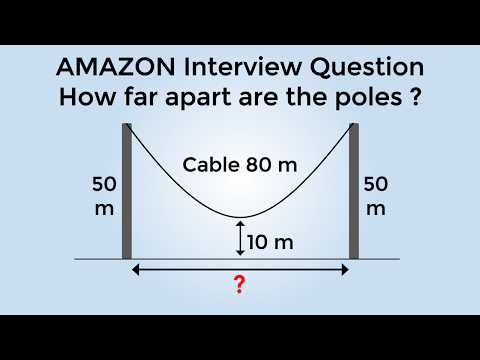
Hey, this is Presh Tall Walker. A version of this problem was used as an interview question. A cable of 80 meters is hanging from the top of two poles that are both 50 meters from the ground. What is the distance between the two poles to one decimal place if the center of the cable is 20 meters above the ground and 10 meters above the ground? Now, to be more specific, a version of problem B was asked during an interview, but I've included problem A because it's interesting mathematically. Can you figure it out? Give this problem a try and when you're ready, keep watching the video for a solution. Music So, let's solve the case of 20 meters above the ground. We have two poles of 50 meters each and we have a hanging cable that's 80 meters long. The center of this cable is 20 meters from the ground and we want to solve for the distance between the two poles. Now, I'll admit I had forgotten how to solve this kind of problem, so I had to look up some formulas online. Many of the websites referred to the physics interpretation, which involved weights and tensions, and I just wanted to get to some of the mathematical formulas. So, I found a great reference from Neil Chatterjee and Bob Donita, "The Hanging Cable Problem for Practical Applications" in the Atlantic Electronic Journal of Mathematics. I provided a link in the video description and I recommend you check it out. So, we'll solve this problem using symmetry and a convenient coordinate system. First, we'll split up the cable into two lengths of 40. Next, we'll consider only the distance from the center of the cable to one of the poles. We can then double that distance to get the...