Can Form 8655 Reflected 2024

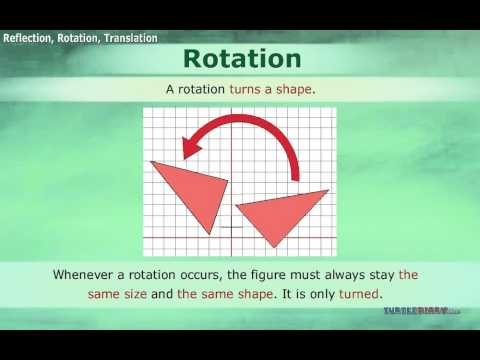
Reflection, rotation, and translation are three basic transformations that can be ed on a shape. These transformations can move the shape without altering its shape or size. A reflection flips a shape to create a mirror image. In the given example, the triangle on the right has been reflected over the dotted line, resulting in a mirror image. The vertices of the triangle (A, B, and C) have been flipped over the dotted line to create the mirror image, which can be seen as another triangle with vertices A', B', and C'. The second figure, called the image, is exactly opposite to the original figure. This can be related to looking in a mirror, where everything appears in the opposite direction. The dotted line is referred to as the line of reflection, axis of reflection, or mirror line. It can be observed that the original point A and the new point A' are equidistant, three units away from the line of reflection. The same holds true for point B (one unit away) and point C (three units away). In a reflection, each set of corresponding points must be equidistant from the line of reflection. Reflections are commonly observed in mirrors, but they can also occur in water. However, reflections in water are not technically mathematical reflections because they are often distorted and not of the exact size and shape. A rotation involves turning a shape around a point. In the example, the triangle has been rotated counterclockwise. Rotations can occur by a few or significant degrees. The shape stays the same in terms of size and shape, but it is simply turned. The point around which the shape is rotated is marked with crosshairs in the given example. If a shape is rotated back to its original position, it is...